Magnitude Frequency Distribution
In seismic hazard analysis, magnitude frequency distribution (MFD) is one of the important parameter that must be considered. The MFD is used for estimating the number of earthquakes (occurrence rate) of each magnitude bin for a region of interest that follows the Gutenberg-Richter’s Law,
\[log_{10} N (\ge M) = a - bM_c\]or
\[N (\ge M) = 10^{a - bM}\]where the \(N (\ge M)\) is the number of earthquakes that have magnitude greater than \(M\), \(M_c\) is the magnitude of completeness, \(a\) and \(b\) are the statistical seismicity parameters that describe the seismicity activity rate and small-large event ratio, respectively. The \(b\) value has a typical value of 1 in global. The MFD data is estimated from the earthquake catalog and it presents by two information, non-cumulative and cumulative, as shown in Figure 1 below.
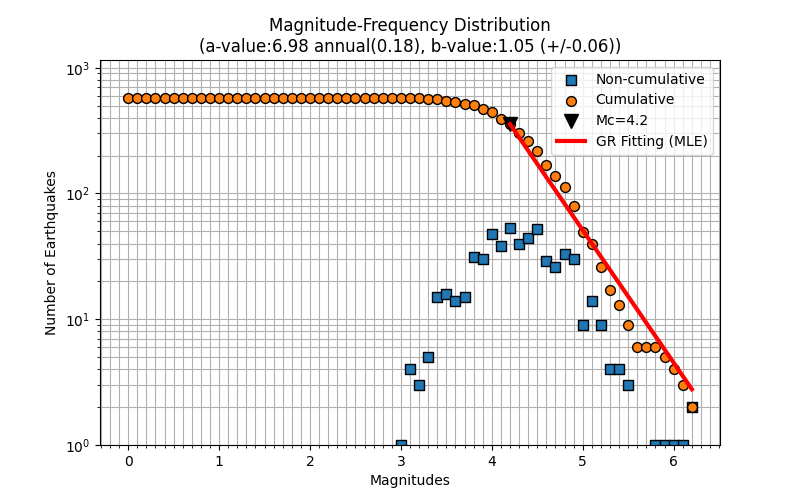
For a simple calculation illustration, assuming \(a = 1\), \(b = 1\) and \(M_c = 0\), we can easily calculate the number of earthquakes that are greater than \(M_c = 0\) by
\[log_{10} N (\ge M) = a - bM_c\] \[log_{10} N (\ge M=0) = 1 - 1 * 0\] \[log_{10} N (\ge M=0) = 1 - 0 = 1\] \[N (\ge M=0) = 10^1 = 10\]This calculation estimated 10 cumulative earthquakes that have a magnitude greater than 0. Now, we try to change \(M_c = 1\) and keep the same value for the rest of the parameters.
\[log_{10} N (\ge M) = a - bM_c\] \[log_{10} N (\ge M=1) = 1 - 1 * 1\] \[log_{10} N (\ge M=1) = 1 - 1 = 0\] \[N (\ge M=0) = 10^0 = 1\]The number of earthquakes decreases by 10 times with increased the \(M_c\). This information tells us that the events with large magnitude occur less frequently and have a lower occurrence rate compared to the events that have low and medium magnitude. As illustrated in Figure 1 above, the number of earthquakes of magnitude above 6 is about 3 events, which is lower than the number of earthquakes of magnitude above 4, which has approximately 400 events.
In the real case, the \(b\) value can be calculated by using Maximum-Likelihood Estimation (MLE), proposed by Aki K, 1965 as written in Equation below
\[b = \frac {log_{10} e} {\bar M - M_c}\]where \(\bar M\) is the mean of magnitude. Furthermore, the \(a\) value can be calculated by using the GR’s Law as mentioned in the equation above. We can also apply simple linear regression to calculate the \(a\) and \(b\) values. The \(M_c\) is then estimated based on the higher frequency number of non-cumulative earthquake distribution. The \(M_c\) becomes a lower magnitude boundary for seismic hazard analysis.
This approach is suitable for regions or areas that have a large seismicity distribution, such as a subduction zone or background seismicity. For the seismicity around a fault, it is suggested to estimate the magnitude frequency distribution or occurrence rate by using Characteristic Earthquake Distribution, proposed by Youngs-Coppersmith, 1985.
The MFD calculation by using MLE and Gutenberg-Richter’s Law can be done by using seisliby.
References
- B. Gutenberg, C. F. Richter; Frequency of earthquakes in California. Bulletin of the Seismological Society of America 1944;; 34 (4): 185–188. doi: https://doi.org/10.1785/BSSA0340040185
- Aki, K. (1965). 17. Maximum Likelihood Estimate of b in the Formula logN=a-bM and its Confidence Limits. 43(2), 237–239. https://repository.dl.itc.u-tokyo.ac.jp/records/33631
- Robert R. Youngs, Kevin J. Coppersmith; Implications of fault slip rates and earthquake recurrence models to probabilistic seismic hazard estimates. Bulletin of the Seismological Society of America 1985;; 75 (4): 939–964. doi: https://doi.org/10.1785/BSSA0750040939